函数图象平移与伸缩的通解
对于函数图象的平移与伸缩问题,传统的处置手法过于冗杂,记忆量大,难于学会.本文试图用代换的手法将它作一般性的探讨.
1、函数图象的平移
事实上,设函数![]() 的图象,向右平移
的图象,向右平移![]() 个单位,得到的图象的分析式是
个单位,得到的图象的分析式是![]() ,令点
,令点![]() 是
是![]() 的图象上任一点,点
的图象上任一点,点![]() 向右平移
向右平移![]() 个单位得点
个单位得点![]() ,则点
,则点![]() 在
在![]() 的图象上,且
的图象上,且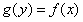 ,有
,有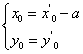 ,于是,把函数
,于是,把函数![]() 的图象,向右平移
的图象,向右平移![]() 个单位,得到的图象的分析式是
个单位,得到的图象的分析式是![]() (即以
(即以![]() 代换
代换![]() ).
).
大家概念:当![]() 时,表示向右平移;当
时,表示向右平移;当![]() 时,表示向左平移.
时,表示向左平移.
例1 函数![]() 是偶函数,则函数
是偶函数,则函数![]() 的对称轴是
的对称轴是
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
解:函数![]() 是偶函数,∴其对称轴为
是偶函数,∴其对称轴为![]() ,以
,以![]() 代换
代换![]() ,有
,有![]() ,
,
令![]() ,解得
,解得![]() ,故函数
,故函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,其对称轴
的图象,其对称轴![]() 也相应地向左平移了
也相应地向左平移了![]() 个单位,故选D.
个单位,故选D.
例2 要得到函数![]() 的图象,仅需将函数
的图象,仅需将函数![]() 的图象
的图象
A. 向左平移![]() 个单位 B. 向右平移
个单位 B. 向右平移![]() 个单位
个单位
C. 向左平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
解:∵![]() ,而在
,而在![]() 中,以
中,以![]() 代换
代换![]() ,有
,有![]() .令
.令![]() ,解得
,解得![]() .故选A.
.故选A.
办法2、![]() .在
.在![]() 中,以
中,以![]() 代换
代换![]() ,
,
有![]() ,令
,令![]() ,解得
,解得![]() .故选A.
.故选A.
同样地,把函数![]() 的图象,向右平移
的图象,向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,得到的图象的分析式是
个单位,得到的图象的分析式是![]() (即以
(即以![]() ,
,![]() 分别代换
分别代换![]() ,
,![]() ).
).
同样,大家概念:当![]() 时,表示向上平移;当
时,表示向上平移;当![]() 时,表示向下平移.
时,表示向下平移.
例3 函数![]() 的图象,经过什么样的平移变换得到函数
的图象,经过什么样的平移变换得到函数![]() 的图象?
的图象?
解:在![]() 中,以
中,以![]() ,
,![]() 分别代换
分别代换![]() ,
,![]() ,有
,有![]() .
.
即![]() ,经对比,有
,经对比,有 ,解得
,解得 .故把函数
.故把函数![]() 的图象,向左平移
的图象,向左平移![]() 个单位,再向上平移3个单位,便得函数
个单位,再向上平移3个单位,便得函数![]() 的图象.
的图象.
2、函数图象的伸缩与平移
事实上,设把函数![]() 的图象的横坐标伸长到原来的
的图象的横坐标伸长到原来的![]() 倍(纵坐标不变),得到的图象的分析式是
倍(纵坐标不变),得到的图象的分析式是![]() ,
,
令点![]() 是
是![]() 的图象上任一点,点
的图象上任一点,点![]() 的横坐标伸长到原来的
的横坐标伸长到原来的![]() 倍,得点
倍,得点![]() ,则点
,则点![]() 在
在![]() 的图象上,且
的图象上,且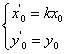 ,有
,有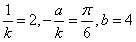 ,
,
于是,设把函数![]() 的图象的横坐标伸长到原来的
的图象的横坐标伸长到原来的![]() 倍(纵坐标不变),得到的图象的分析式是
倍(纵坐标不变),得到的图象的分析式是![]() (即以
(即以![]() 代换
代换![]() ).
).
大家概念:当![]() 时,表示伸长;当
时,表示伸长;当![]() 时,表示缩短.
时,表示缩短.
例4 函数![]() 的图象,经过什么样的平移和伸缩变换得到函数
的图象,经过什么样的平移和伸缩变换得到函数![]() 的图象?
的图象?
解:(先平移后伸缩)在![]() 中,以
中,以![]() ,
,![]() 分别代换
分别代换![]() ,
,![]() ,有
,有![]() ,再以
,再以![]() 代换
代换![]() ,有
,有![]() ,即
,即![]() .对比有
.对比有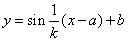 ,
,
得![]() .即把函数
.即把函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移4个单位,后将横坐标缩短到原来的
个单位,再向上平移4个单位,后将横坐标缩短到原来的![]() 倍(纵坐标不变),可得函数
倍(纵坐标不变),可得函数![]() 的图象.
的图象.
办法2、(先伸缩后平移)在![]() 中,以
中,以![]() 代换
代换![]() ,有
,有![]() ,再以
,再以![]() ,
,![]() 分别代换
分别代换![]() ,
,![]() ,得
,得![]() ,即
,即![]() 于是
于是 ,
,
得![]() ,∴
,∴![]() .即把函数
.即把函数![]() 的图象横坐标缩短到原来的
的图象横坐标缩短到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位,后向上平移4个单位,可得函数
个单位,后向上平移4个单位,可得函数![]() 的图象.
的图象.
把函数![]() 的图象的横坐标与纵坐标分别伸长到原来的
的图象的横坐标与纵坐标分别伸长到原来的![]() 倍,得到的图象的分析式是
倍,得到的图象的分析式是![]() (即分别以
(即分别以![]() ,
,![]() 代换
代换![]() ).
).
大家概念:当![]() 时,表示伸长;当
时,表示伸长;当![]() 时,表示缩短.
时,表示缩短.
例5 已知函数![]() ,将
,将![]() 的图象向左平移1个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数
的图象向左平移1个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数![]() 的图象.
的图象.
(I)求![]() 的分析式及概念域; (II)求
的分析式及概念域; (II)求![]() 的最大值.
的最大值.
解:(I)依题意,在![]() 中,以
中,以![]() (即
(即![]() )代换
)代换![]() ,得
,得![]() ,即
,即![]() ,再以
,再以![]() 代换
代换![]() ,得
,得![]() .故得
.故得![]() …….下略.
…….下略.
例6 函数![]() 的图象,经过什么样的变换得到函数
的图象,经过什么样的变换得到函数![]() 的图象?
的图象?
解:(先伸缩后平移)在![]() 中,分别以
中,分别以![]() ,
,![]() 代换
代换![]() ,有
,有![]() ,再以
,再以![]() 代换
代换![]() ,得
,得![]() ,即
,即![]() ,令
,令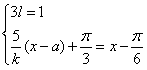 ,得
,得![]() .故把函数
.故把函数![]() 的图象,横坐标伸长到原来的5倍(纵坐标不变),再将纵坐标缩短到原来的
的图象,横坐标伸长到原来的5倍(纵坐标不变),再将纵坐标缩短到原来的![]() 倍(横坐标不变),后向右平移
倍(横坐标不变),后向右平移![]() 个单位,即得函数
个单位,即得函数![]() 的图象.
的图象.
(本题也可“先平移后伸缩”行变换)







